StoSpecRep
Spectral representation for stochastic processes
- The latest release can be accessed via
.
- It has been hosted on
.
Introduction
Stochastic processes are widely adopted in many domains to deal with problems which are stochastic in nature and involve strong nonlinearity, nonstationarity, and uncertain system problems1. Capturing the nonstationarity plays a central role in characterising many environmental processes (e.g. earthquake ground motion or wind) and realistically reflect the response process of engineering structures under stochastic excitations2.
formulation
In this section, a brief review of the theory of the spectral representation of stochastic processes (stationary and non-stationary) is outlined. In particular, focus is on power spectral estimation and simulation of the corresponding processes. A general non-stationary random process, with respect to a family of oscillatory functions, can be represented in the form:
\[X_{t} = \int_{-\infty}^{\infty} A(\omega, t) e^{i \omega t} \text{d} Z(\omega)\]where \(\phi_{t}(\omega)= A(\omega, t) e^{i \omega t}\) represent the oscillatory functions, of which \(A(\omega, t)\) suggests a slowly varying and frequency-dependent modulating function and $Z(\omega)$ is an orthogonal process; \(\{X_{t}\}\) is termed as oscillatory processes whose (two-sided) evolutionary power spectral density is further given as:
\[S(\omega, t) = |A(\omega, t)|^2 S(\omega)\]where \(S(\omega)\) represents the power spectral density function in the case of a stationary process with a family of complex exponentials, i.e., \(\phi_{t}(\omega)=e^{i \omega t}\). The semi-stationary property due to the slowly-changing spectra premise facilitates the practical estimation of the evolutionary spectra given a realization record via non-stationary time-frequency methods, e.g. wavelet transforms. Inversely, a versatile formula for generating sample realizations compatible with the stochastic process is given by spectral representation method (SRM):
\[x^{(i)}(t) = \sqrt{2} \sum_{n=0}^{N-1} \sqrt{2 S(\omega_{n}, t) \Delta \omega} \cos(\omega_{n} t + \Phi^{(i)}_{n})\]where \(x^{(i)}(t)\) is a sample simulation, $\Phi^{(i)}$ is the set of independent random phase angles, distributed uniformly over the interval \([0, 2 \pi]\), for the $i$th sample realizations; \(N\) and \(\Delta{\omega}\) relate to the discretization of the frequency domain.
functionality
- Estimating EPSD or PSD from realizations via wavelet transform;
- Implementing Spetral Representation Method given EPSD;
Example usages
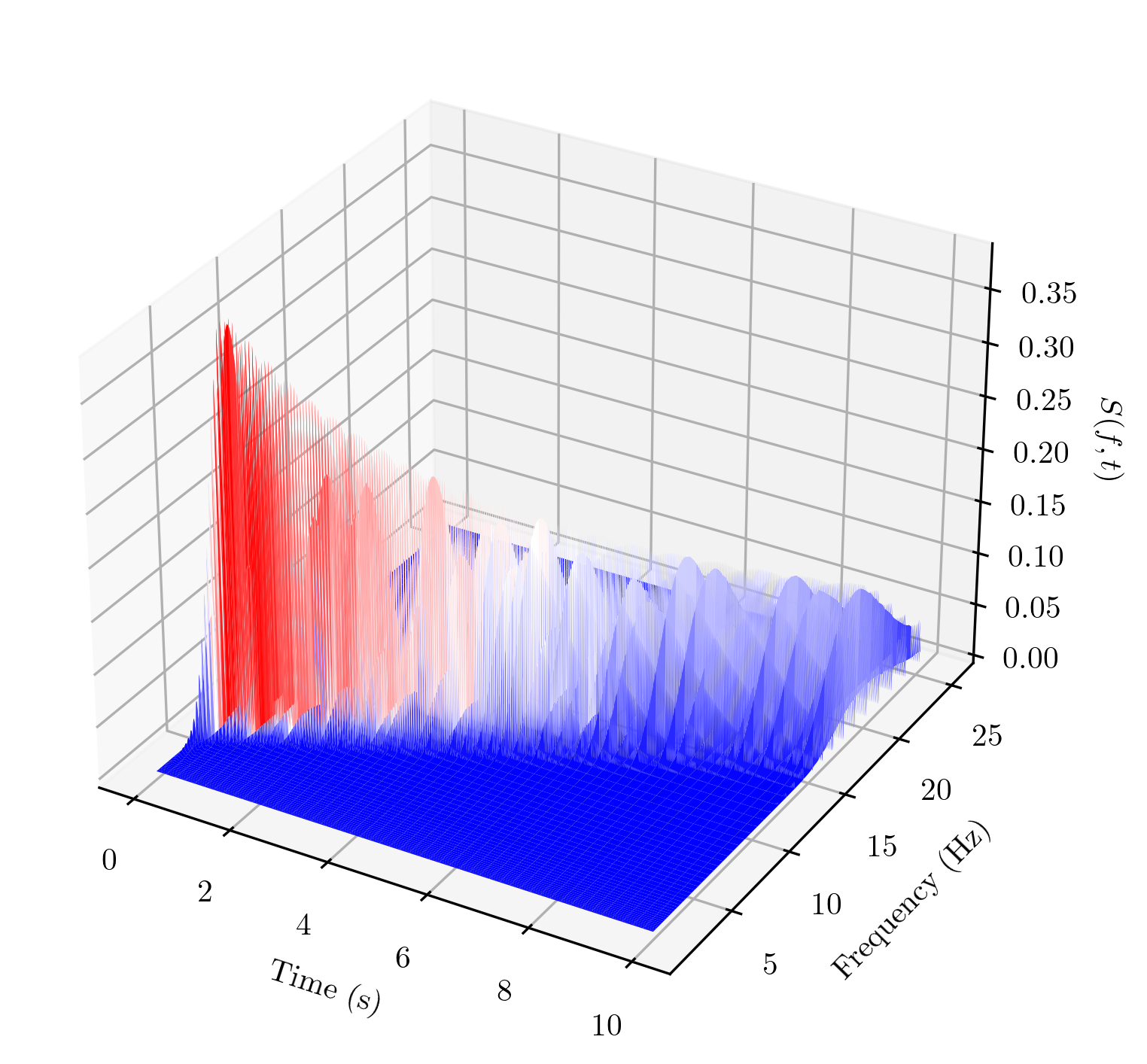
1. chirp signal
An illustrating example of a linear chirp signal whose frequency spectrum is changing with time.
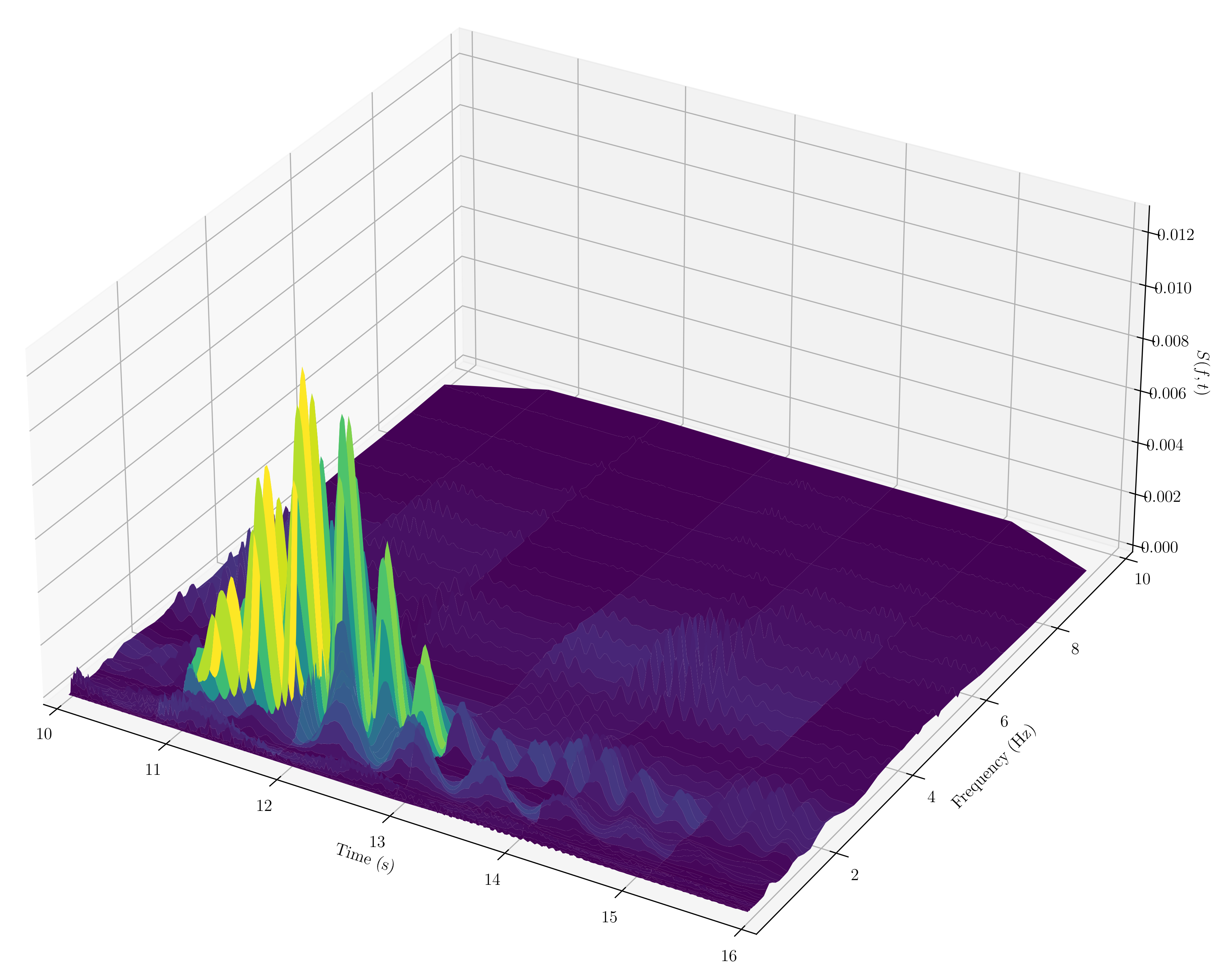
2. El centro earthquake
The ‘hello world’ example of an earthquake recording, showing its estimated evolutionary power spectrum. Many spectral results based on this example can be found in the literature.
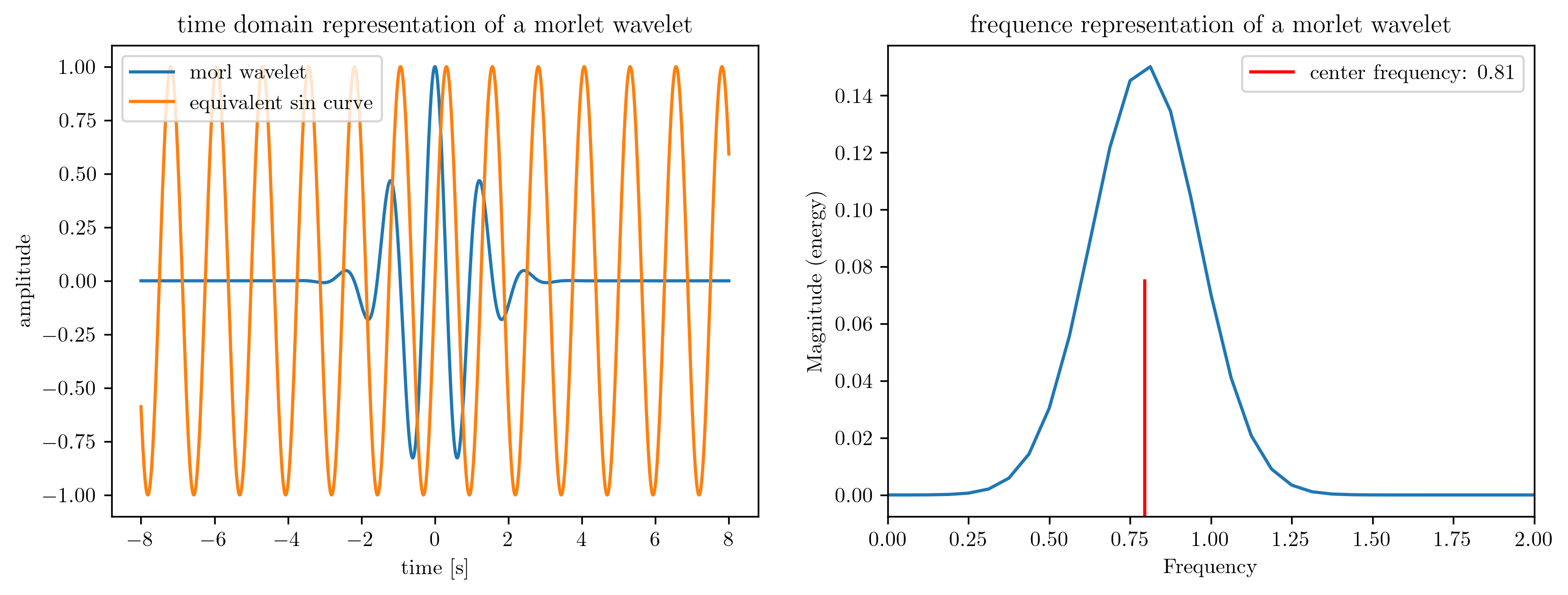
Morlet wavelet introduction
A practical introduction to Wavelet transform (morlet) can be found in Morlet wavelet basics
