KTnSRM

Spectral power density models and Spectral Representation Method

  • The latest release can be accessed via DOI.
  • It has been hosted on Repo.

Introduction

Stochastic process models are responsible for characterising ground motions, representing the stochastic excitations applied upon engineering structures1. To this end, a series of power spectral density models are developed and employed in stochastic dynamic analysis2. Notably, Kanai Tajimi model plays a foundational role3. Beyond which, nonstationary model attract more attention in recent years.

functionality

  • Define a base Kanai Tajimi model;
  • Define both separable and non-separable evolutionary power spectral density models;
  • Generate sample realizations via the Spectral Representation Method;
  • A general framework enabling easy addition of more nonstationary models via subclassing.

Examples

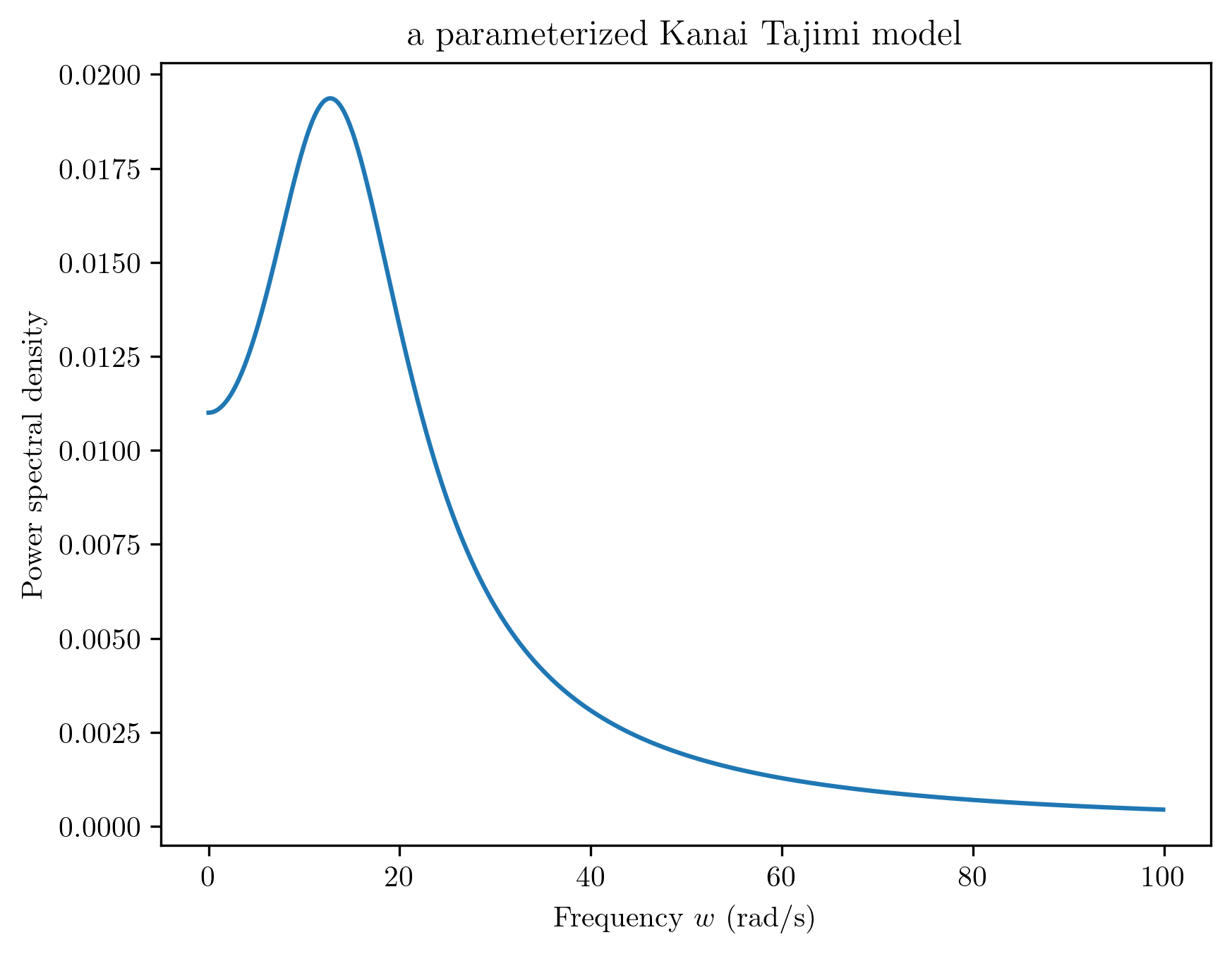
1. Kanai Tajimi PSD model

\[S(\omega) = S_{0} \frac{1+[2 \zeta (\omega/\omega_{g})]^2}{[1-(\omega/\omega_{g})^2]^2+[2 \zeta (\omega/\omega_{g})]^2}\]

where \(w_{g}=5 \pi\) rad/s; \(\zeta\) = 0.63; \(S_{0}\) = 0.011;

Kanai Tajimi PSD

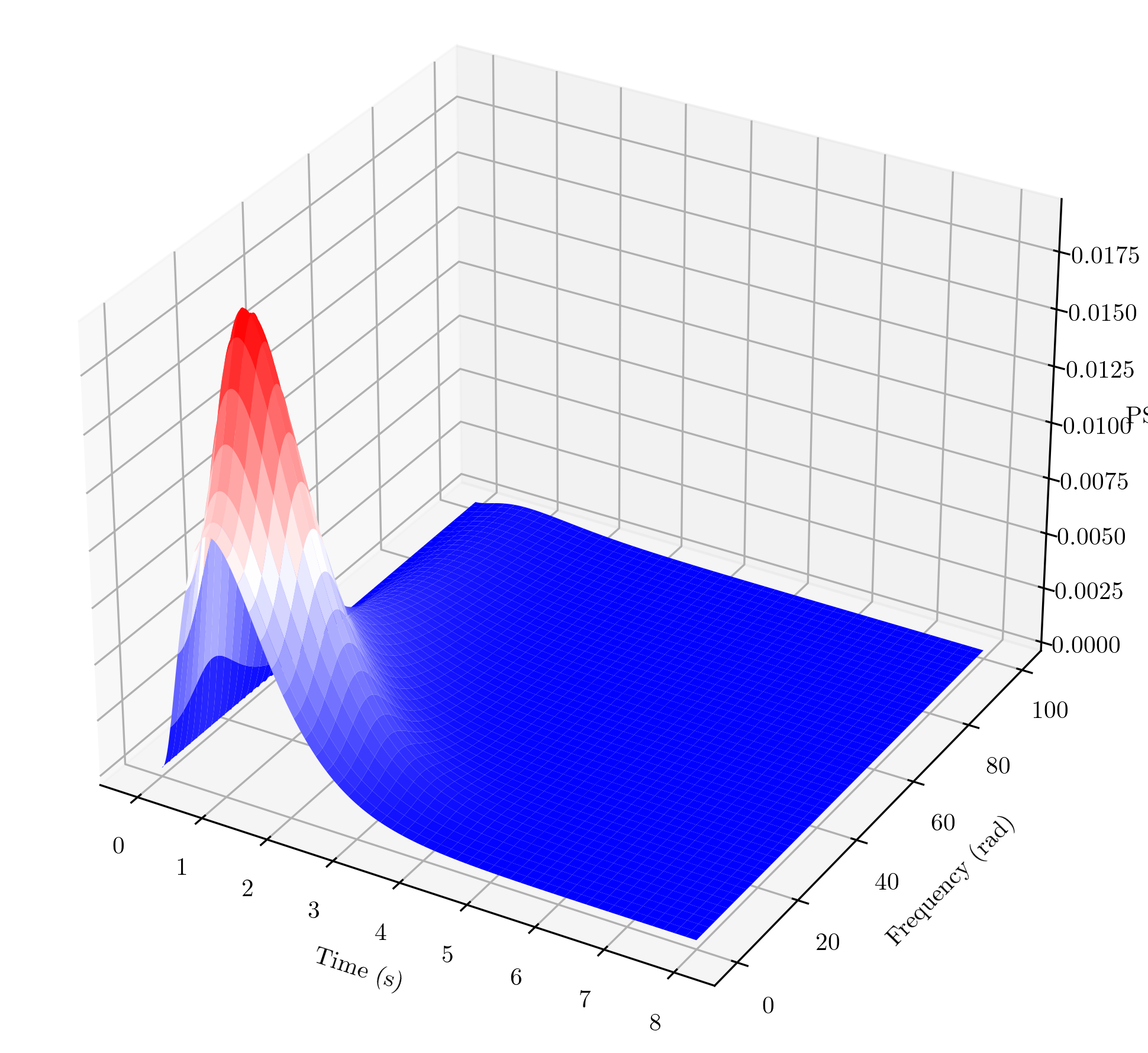
2. separable EPSD

Define an evolutionary spectrum in the form \(S(\omega, t)=g(t)^2S(\omega)\)

with an example of modulating function: \(g(t)=b(e^{-ct} - e^{-2ct})\) where $b$=4, $c$=0.8

Example non-separable evolutionary power spectral function

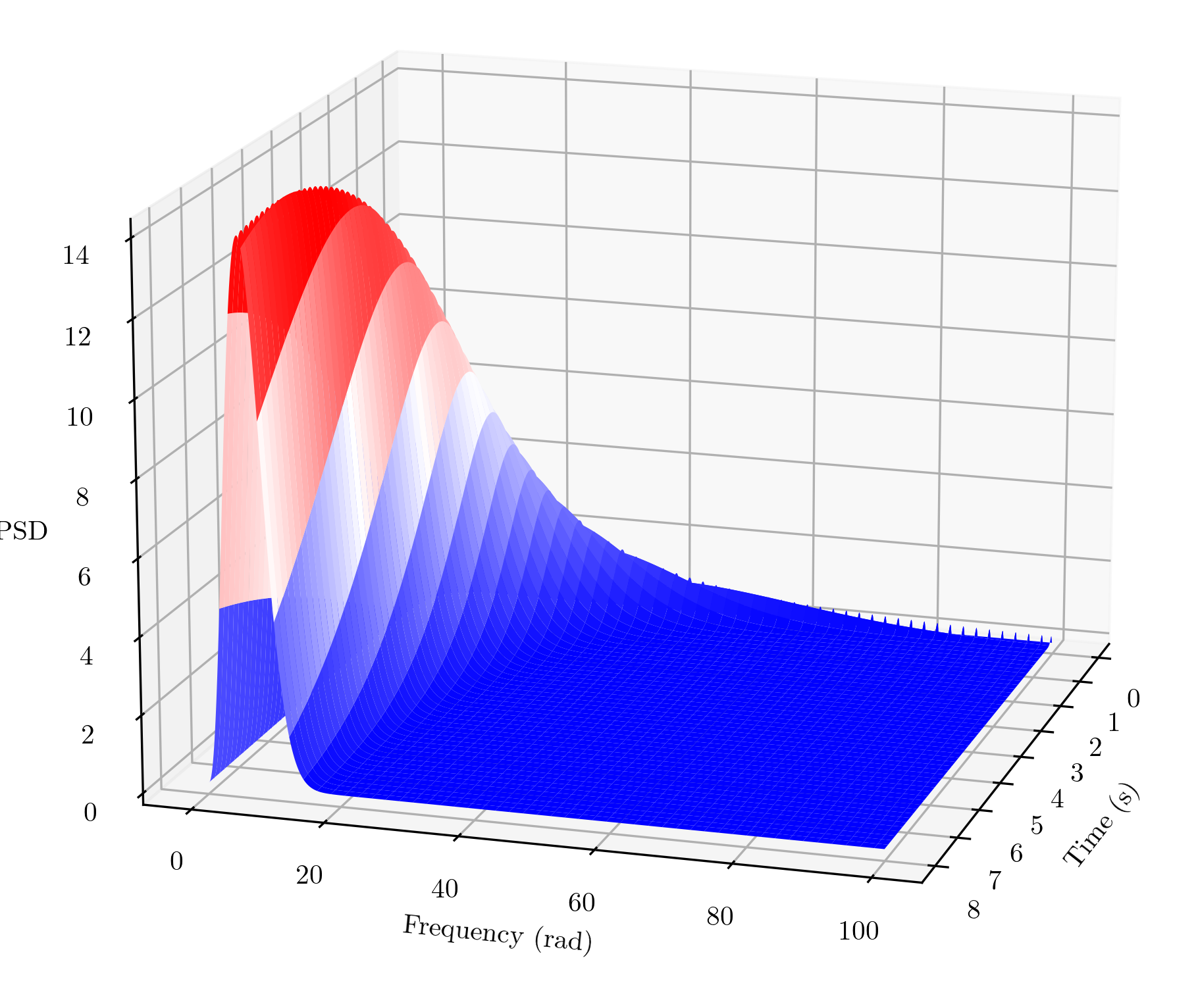
3. non-separable EPSD

An evolutionary spectrum with fully coupled time and frequency nonstationarity. Define an example EPS: \(S(\omega, t) =\frac{\omega^2}{5 \pi} e^{-0.15t} t^{2} e^{-(\frac{\omega}{5 \pi})^2 t}\)

Example separable evolutionary power spectral function
  1. Spectral Representation Method

  1. Kiureghian etc. Nonlinear stochastic dynamic analysis for performance-basedearthquake engineering. ↩

  2. Conte and Peng. Fully nonstationary analytical earthquake ground-motion model. ↩

  3. Lai etc. Statistical characterization of strong ground motions using power spectral density function. ↩