Imputation is no picnic
Uncertainty quantification over spectral representation of stochastic processes in the presence of missing data
Introduction
Missing data is an ubiquitous problem of various engineering and physical fields, in which incompleness may present in the observational recordings or engineering monitoring data. In fact, it is pervasive in virtually any discipline where in situ measurements are collected and transferred, as a result of abundant practical reasons causing intermittent failure, such as sensor failure or incompetence, temporary transmission loss for real-time data, plus numerous other reasons including sensor maintenance, usage, data acquisition restrictions and or data-corruption, see It is therefore vital for safety-critical systems operated by decision-makings on the basis of real-time data streams (e.g. autonomous driving) to be robust under unexpected sensor failure.
Three challenges
Stochastic processes are widely adopted to characterise time-dependent data which are random in nature and involve strong nonstationarity, as well as to model system responses that involve highly nonstationarity and uncertain system parameters. We seek a probabilistic spectral representation of the underlying stochastic processes even in the presense of missing data, and investigate the propagation of uncertainties from imperfect observations all the way through the computational pipeline.
However, we note there are three main challenges in this noble cause:
(I) It’s practically impossible for the certain event/scenario/incident under recording to be reevaluated (let bygones be bygones ![]() ) hence almost impossible to reconstruct the missing samples not measured with certainty. Uncertainty quantification plays a key role in reflecting the inherent uncertainty of the missing data and the downstream models.
) hence almost impossible to reconstruct the missing samples not measured with certainty. Uncertainty quantification plays a key role in reflecting the inherent uncertainty of the missing data and the downstream models.
(II) most of current approaches are developed on the stationary assumption hence inadequate to reflect the nonstationary properties of most real world processes.
(III) most importantly, most of current approaches are still significantly bounded by a ceiling in performance since they are merely driven by the very limited information contained in the incomplete data.
Our proposed solution and two frameworks
Due to the limit of data quality, fully data-driven methods are bounded to a ceiling performance. As such, our idea is rooted in the incorporation of prior domain knowledge to guide the learning/inference and mitigate the impacts of data problems, thereby producing robust and informed models.
Particularly, in response to the three challenges, we propose knowledge-guided Bayesian frameworks. Depending on the level of information incorporated, two frameworks are proposed. We first proposed a Augmented-Learning framework (i) takes advantage of a-priori knowledge of the underlying process, enabling to incorporate additional information (physics-based knowledge) into the modelling. (ii) accounts for uncertainty throughout the framework, allowing to provide a host of outputs in a probabilistic manner (e.g. reconstructions, spectral representations, and stochastic-process sample generations). (iii) applicable to nonstationary processes. Beyond that, an extension is further proposed
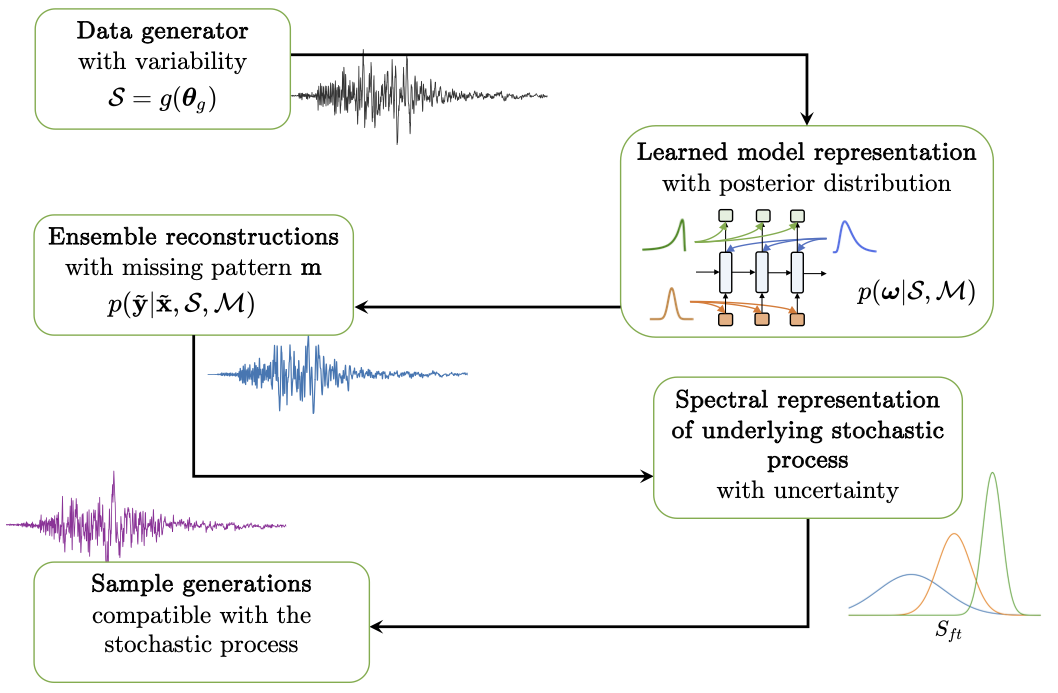
We build on the premise that prior knowledge could provide general yet insightful prior expectations of the observation (with variaibility) of the physical process. The a-priori information is addressed by generating simulations based on the domain knowledge represented by \(\boldsymbol{\theta}_{g}\).
specifically, \(\boldsymbol{\theta}_{g} = (\theta_{1}, \dots, \theta_{n})\) represents a random vector of relevant physical parameters, each component of which stands for a random variable. \(g(\cdot)\) represents a generator function, which may just be a model with physics aspects capable of generating stochastic simulations accordingly. Collectively the corresponding probability distribution \(p(\boldsymbol{\theta}_{g})\) would reflect the variability of the simulations embedded in our prior belief.
Given the data represented by those physics-informed simulations, Bayesian recurrent neural network models \(\mathcal{M}\) are trained as probabilistic model representations of the underlying process, whereby the imputation of missing data is conducted as predictions in a recursive manner. Importantly, the epistemic uncertainties of the learned model representations are addressed by putting probability distributions over the model parameters \(\boldsymbol{\omega}\) of neural nets, thus giving rise to the posterior distribution \(p(\boldsymbol{\omega}| \mathcal{S}, \mathcal{M})\) through the Bayesian inference, as given below:
\[p(\boldsymbol{\omega}|\mathcal{S}, \mathcal{M}) = \frac{p(\mathcal{S}|\boldsymbol{\omega}, \mathcal{M}) p(\boldsymbol{\omega}|\mathcal{M})}{p(\mathcal{S}|\mathcal{M})} \propto p(\mathcal{S}|\boldsymbol{\omega}, \mathcal{M}) p(\boldsymbol{\omega}|\mathcal{M})\]This marks a key step of the proposed framework, where a probabilistic representation of the underlying processes is learned by recurrent neural network models and further used to reconstruct the incomplete observations. Besides, in this study we also present investigations and comparisons of a few neural network architectures in this regard. With the posterior distribution, an ensemble of recurrent imputations can be obtained by marginalizing out the parameter space, as follows:
\[\mathcal{R} = \int p(\tilde{\mathbf{y}} | \tilde{\mathbf{x}}, \boldsymbol{\omega}) p(\boldsymbol{\omega}| \mathcal{S}) \text{d} \boldsymbol{\omega} \label{eq:predictive_distribution}\]where $\tilde{\mathbf{x}}$ represents the missing samples in a specific recording; $\mathcal{R}$ denotes the reconstructed process, practically through an ensemble of reconstructions, which contain both the recurrent imputations $\tilde{\mathbf{y}}$ and existing observations.
Results
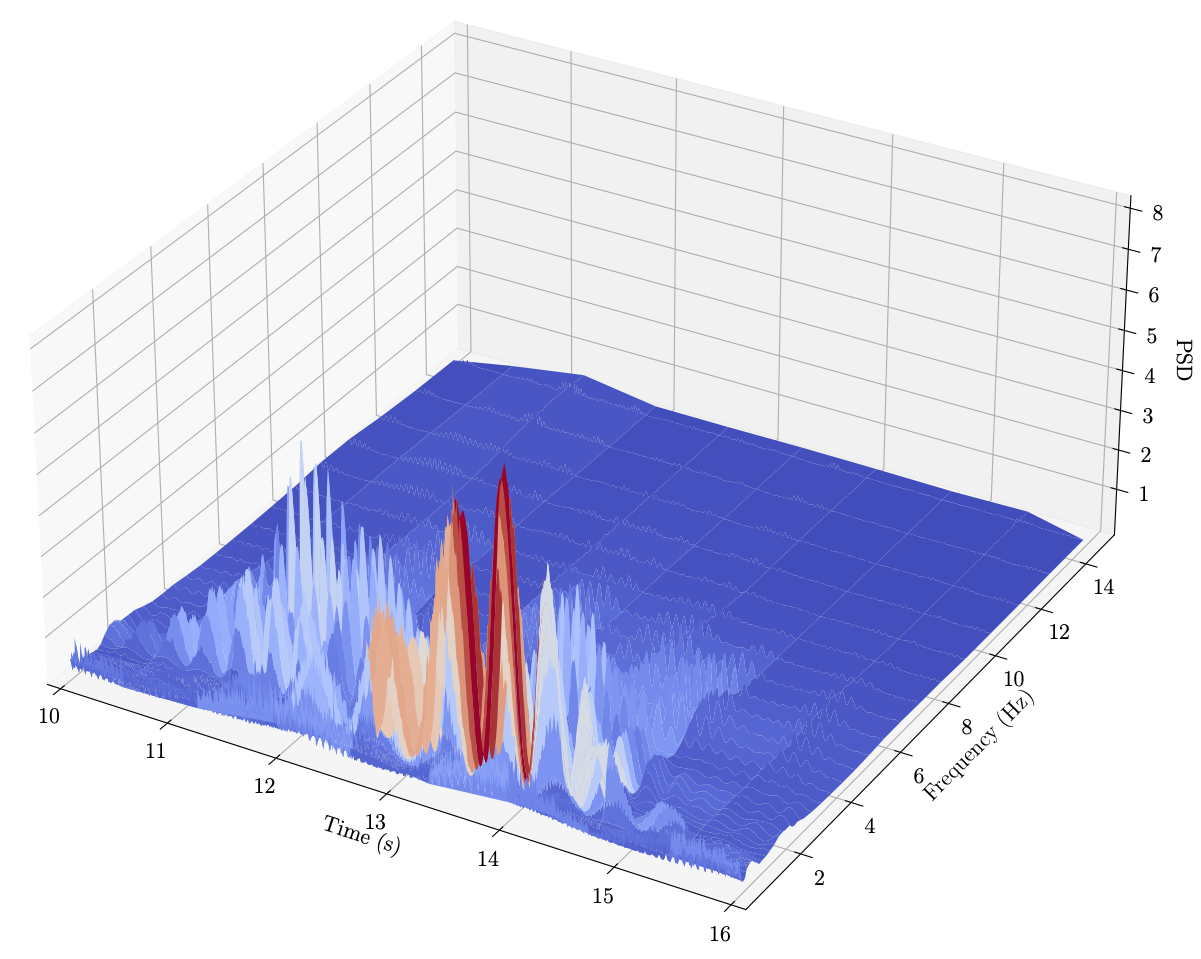
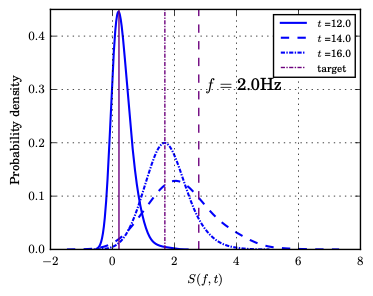
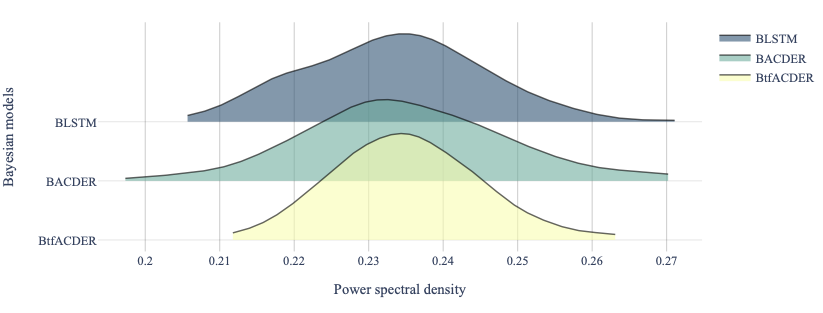
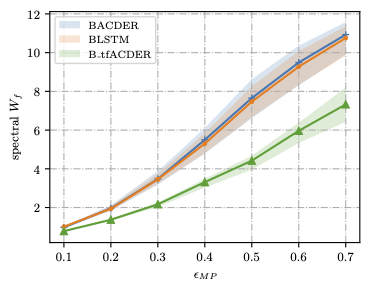
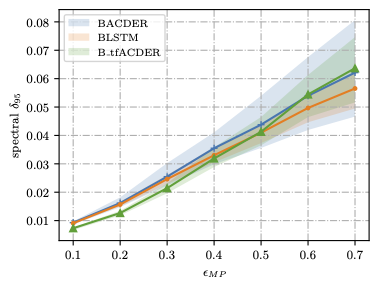
Uncertainty metrics are computed below: